벨만-포드 알고리즘(Bellman-Ford Algorithm)
한 노드에서 다른 노드까지의 최단 거리를 구하는 알고리즘이며, 다익스트라(Dijkstra) 알고리즘 알고리즘과의 차이는 간선의 가중치가 음수일 때도 최단 거리를 구할 수 있다는 점이다.
벨만-포드 vs 다익스트라
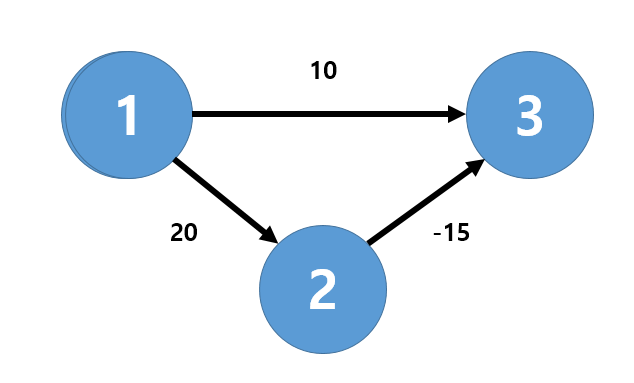
위 그림에서 경로는 cost:10 과 cost:20-15=5 가 있다. 다익스트라 알고리즘을 사용한다면 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 선택하므로 1->3 의 경로를 선택한다. 이처럼 음수 간선이 존재하면 최단 거리를 찾을 수 없는 상황이 발생한다.
반면 벨만-포드 알고리즘을 사용하게 되면 매번 모든 간선을 전부 확인하기 때문에 정확하게 최단 거리를 찾을 수 있게 된다.
다익스트라
매번 방문하지 않은 노드 중 최단 거리가 가장 짧은 노드를 그리디하게 선택하여 한 단계씩 최단 거리를 구해나간다.
음수 간선이 없다면 최적의 해를 찾을 수 있다.
Priority Queue를 사용하는 개선된 다익스트라 알고리즘을 사용한다면 OElogV로 시간복잡도가 빠르다
벨만-포드 알고리즘
매 단계마다 모든 간선을 전부 확인하면서, 모든 노드간의 최단 거리를 구해나간다.
그렇기에 음수 간선이 있어도 최적의 해를 찾을 수 있다. 음수 간선의 순환을 감지할 수 있기 때문이다.
시간복잡도가 O(VE)로 느리다
과정
- 출발 노드를 설정한다
- 최단 거리 테이블을 초기화한다
- 다음의 과정을 (V-1)번 반복한다
- 모든 간선 E개를 하나씩 확인하다
- 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다
만약 음수 간선 순환이 발생하는지 체크하고 싶다면 3번의 과정을 한 번 더 수행한다. 이때 최단 거리 테이블이 갱신된다면 음수 간선 순환이 존재하는 것이다.
음수 간선 순환을 왜 확인할까?
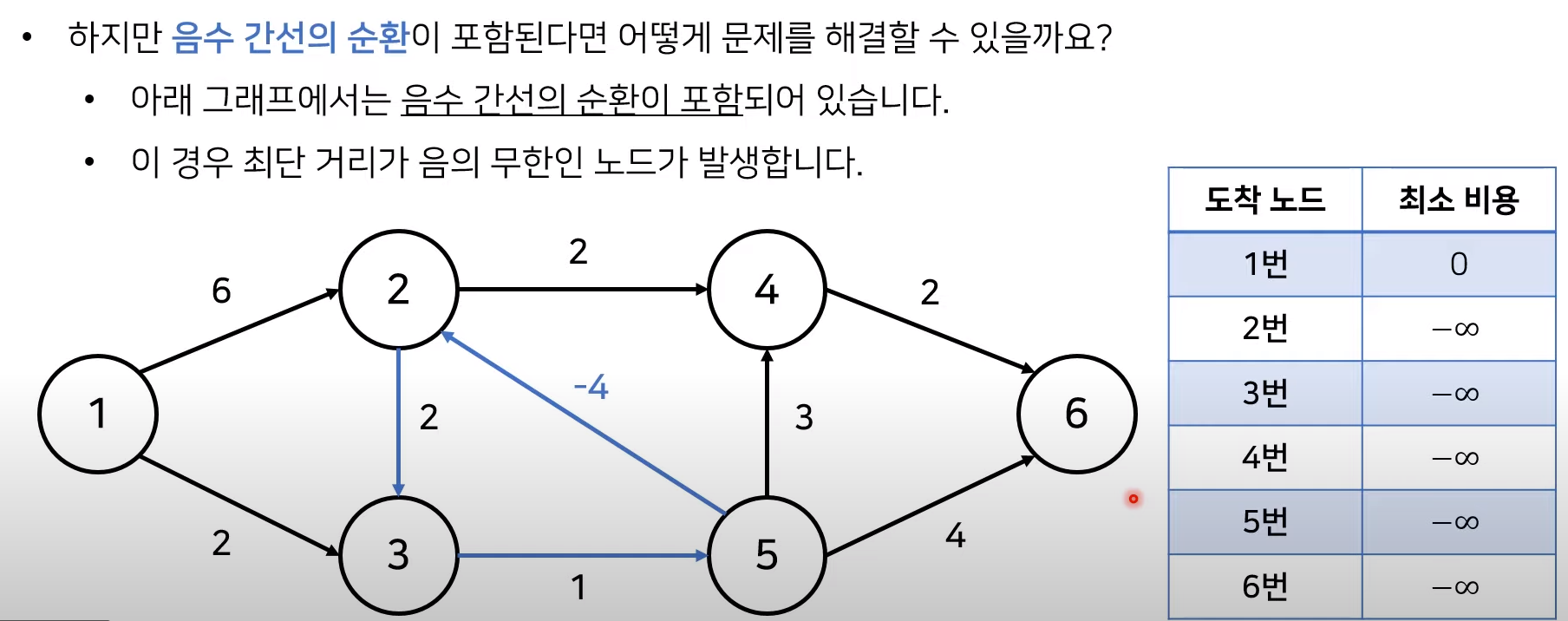
2번 -> 5번으로 가는 경로를 계속 순환하게 되면 비용을 무한히 줄일 수 있게 된다. 이는 1번 노드를 제외한 모든 노드에서도 비용을 무한히 줄일 수 있기 때문에 최단 거리를 구할 수 없게 되므로 꼭 음수 간선 순환을 확인해주어야 한다.
V - 1까지 모든 단계를 진행한 후, 다음 단계인 V번째 단계일 때도 최단 거리 테이블이 갱신된다면 최단 거리를 무한히 줄일려는 시도이므로 음수 간선 순환이 존재한다는 사실을 알 수 있다. 따라서 V번째 단계에서 최단 거리 테이블이 갱신 여부로 음수 간선 순환을 확인할 수 있다.
구현
class Edge {
int v; // 나가는 정점
int w; // 들어오는 정점
int cost;
public Edge(int v, int w, int cost) {
this.v = v;
this.w = w;
this.cost = cost;
}
}
public class Main {
static ArrayList<Edge> graph;
static final int INF = 1000000000;
//정점의 개수, 간선의 개수, 출발지
public static boolean BellmanFord(int n, int m, int start) {
int[] dist = new int[n + 1];
Arrays.fill(dist, INF);
dist[start] = 0;
//정점의 개수만큼 반복
for (int i = 0; i < n; i++) {
//간선의 개수만큼 반복
for (int j = 0; j < m; j++) {
Edge edge = graph.get(j); //현재 간선
//현재 간선의 들어오는 정점에 대해 비교
if (dist[edge.v] != INF && dist[edge.w] > dist[edge.v] + edge.cost) {
dist[edge.w] = dist[edge.v] + edge.cost;
}
}
}
//음수 가중치 확인
for (int i = 0; i < m; i++) {
Edge edge = graph.get(i); //현재 간선
//현재 간선의 들어오는 정점에 대해 비교 -> 더 작은 값 생기면 음수 사이클 존재
if (dist[edge.v] != INF && dist[edge.w] > dist[edge.v] + edge.cost) {
System.out.println("음수 사이클 존재");
return false;
}
}
//출력
for (int i = 1; i < dist.length; i++) {
if (dist[i] == INF)
System.out.print("INF ");
else
System.out.print(dist[i] + " ");
}
return true;
}
public static void main(String[] args) throws IOException {
//그래프 입력받기
BufferedReader bf = new BufferedReader(new InputStreamReader(System.in));
// 정점의 개수, 간선의 개수
int n = Integer.parseInt(bf.readLine());
int m = Integer.parseInt(bf.readLine());
graph = new ArrayList<>();
StringTokenizer st;
for (int i = 0; i < m; i++) {
st = new StringTokenizer(bf.readLine());
int v = Integer.parseInt(st.nextToken());
int w = Integer.parseInt(st.nextToken());
int cost = Integer.parseInt(st.nextToken());
graph.add(new Edge(v, w, cost));
}
//벨만-포드 알고리즘 수행
BellmanFord(n, m, 4);
}
}